Mi is az a geoid? Földrajzórán talán előjön, az egyetemen már ilyen szakokon biztosan. A kicsit pontatlan, de egyszerűbb definíció, hogy "a tengerszint folytatása a szárazföldek alatt". Ha geofizikus jön szembe, akkor persze nem ússzuk meg, hogy el ne mondja: "a Föld nehézségi erőterének a középtengerszinthez tartozó potenciálfelülete". Mivel e sorok írója is ezt a tudományt tanulja, most, a poszt erejéig maradjunk is ennél. Maradjunk, de mit is jelent ez? A nehézségi erőtér, az a Föld tömege által keltett vonzás és a tengely körüli forgás okozta centrifugális erő eredője, vagyis az, ami miatt és amerre a zuhanó testek esnek. A "potenciál" kicsit bonyolultabb, de ha azt mondjuk, hogy azon a felületen, ahol ez azonos, ott munkabefektetés nélkül mozoghatunk. Ezeket hívjuk potenciálfelületeknek, elvileg a tengerszint (sőt bármilyen folyadékfelszín, legyen az akár a kávénk a csészében) is az: nem véletlen, hogy a hajózás milyen kevés energiát igényel.
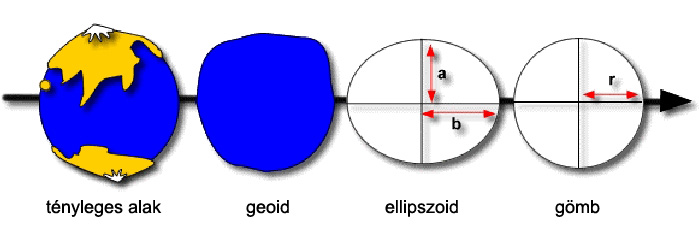
A Föld tényleges alakja (amelyet a "tengerszint feletti magasság" ír le) mihez képest értendő? A régi görögök gömbfelületnek, Newton és Huygens forgási ellipszoidnak gondolták a tengerfelszín ideális alakját. Gauss 1828-ban egy összetettebb formát javasolt, amelyet 1872-ben Listing geoidnak nevezett el (eredeti forrás)
A "geoid" szó is érdekes, annyit jelent, hogy "földszerű". Már az ókorban is felmerült, Arkhimédész javaslatára, hogy a Föld alakját a tenger szintjéhez kössük, mely feltevése szerint gömb alakot vesz fel. A XVII. század végén Newton és Huygens ismerte fel, hogy a gömbi közelítés nem teljesen fedi a valóságot, ezért inkább forgási ellipszoidot használtak. Később aztán egyértelművé vált, hogy a valódi alak ennél is bonyolultabb.
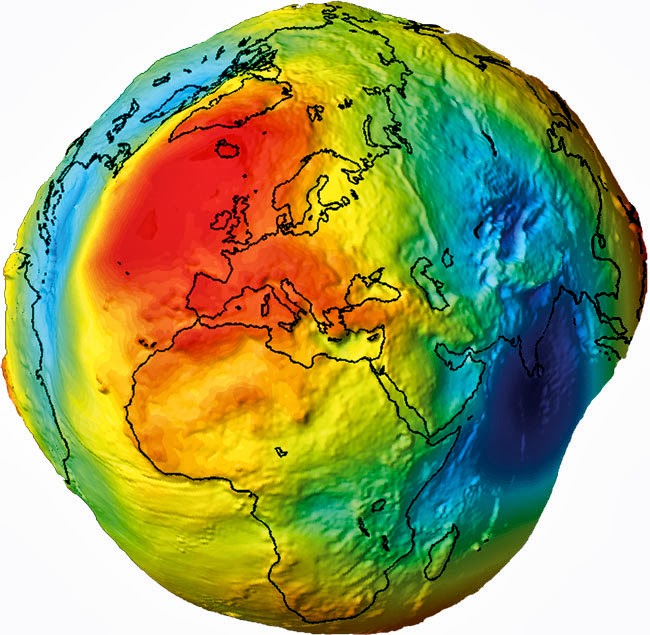
A geoid tényleg ilyen összetett felület: ezen a képen kb. tízezerszeres magassági torzítással. A valóságban a legjobban illeszkedő forgási ellipszoidhoz képest magassági értelemben sehol nem tér el 100 méternél jobban
Ezt Gauss mondta ki 1828-ban. Szerinte a Föld elméleti alakját nem geometriai testhez kell kötni, hanem gyakorlatilag egy újat kell definiálni ehhez: ez lesz a geoid (ezt a nevet később Gauss egyik doktorandusza adta, persze akkor már professzorként). Az első bekezdés jó bonyolult definíciója így Gausstól származik. A potenciál, bár nem szeretnék belebonyolódni, de egy számítható érték, az SI mértékegysége m²/s². Ha egy felület potenciálfelület, akkor ott ez az érték azonos. Meg is mondták az 1980. évi geodéziai rendszerben, hogy a geoidfelülethez tartozó potenciálérték 62636860,850 m²/s².
Engem pedig nagyon érdekelt, hogy ennek van-e valami köze tényleg a tengerszinthez? A tengerek szintjét tengeri vízmércéken, ún. mareográfokon mérik, kb. úgy, ahogy a folyókét is. Ezeken van egy "nulla" és bizonyos időközönként leolvassák, hogy ehhez képest hol is áll a tengerszint. Nyilván megjelenik ebben az árapály, az időjárás (a légnyomás "benyomja" vagy épp "felszippantja" a tengerszintet), hat rá a tengeráramlások rendszere is. Mareográf-adatokra vadásztam tehát, méghozzá olyanokra, amelyeknél a "nulla" szinthez kapcsolható volt olyan adat, amelyből kiszámítható volt annak távolsága a Föld tömegközéppontjától.

Így néz ki egy mareográf: ez épp a Foz do Douro, Portugáliában.
A több száz elérhető mareográfnak alig a tizede volt ilyen. Ha valaki szeretne ilyen adatok közt kutakodni, a Permanent Service for Mean Sea Level oldalán megteheti. A mért tengerszintek, a mareográfok nulla pontjának három dimenziós helyzete és az 1980. évi geodéziai rendszerben használt geoid-modellparaméterek felhasználásával kiszámítottam 25 mareográf esetén a potenciálértéket.
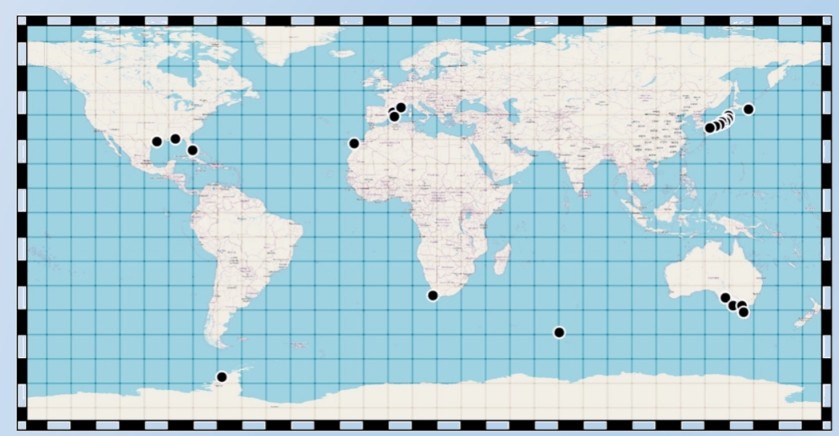
Az általam felhasznált mareográfok helyei
És nem: jelenlegi ismereteim és a számítások alapján a geoid nem illeszkedik pontosan a tengerszinthez, bár az átlagos eltérés a Föld felszínén tényleg lehet nullához közeli. Az eltérések függőleges értelemben néhány tíz méteres nagyságrendet mutatnak. Ez számomra meglepő volt, jobb illeszkedést vártam. Ennek magyarázata az is lehet egyrészt az, hogy az 1980. évi rendszer potenciálértékét nem a fizikai tengerszintből, hanem a Föld egyéb tulajdonságaiból (elsősorban az egyenlítői sugarának középértékéből és lapultságából) vezették le.
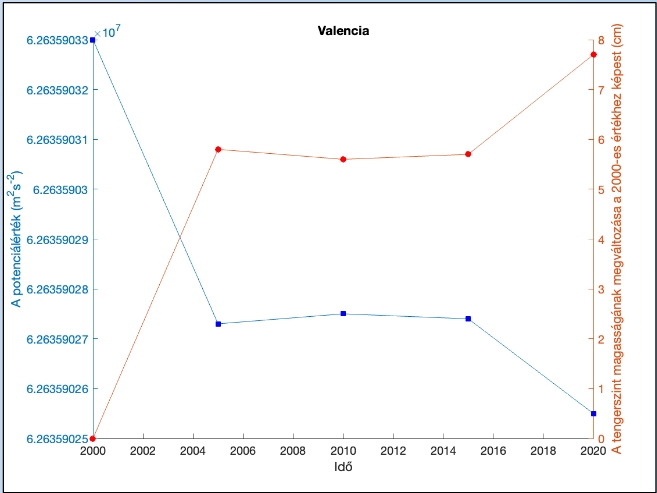
A valenciai (Spanyolország) mareográf hosszú távú tengerszint-adatsora 2000-2020 között: enyhe szintemelkedés, de a középső, mintegy évtizedes periódusban érdemi változás nélkül
Ha már hozzáfértem évtizedes hosszúságú tengerszint-adatokhoz (ismétlem: a fenti linken bárki megteheti), megnéztem, hogy időben milyen tendenciát mutatnak a hosszú távú változások. A tendencia szinte mindenütt emelkedő, érdekes módon viszont nem azonos: Japán nyugati partjain évente mm, míg Spanyolország földközi-tengeri partján ennek kb. kétszerese.
Cziráki Kamilla geofizikus mesterszakos hallgató (ELTE Geofizikai és Űrtudományi Tanszék)
A Kulturális és Innovációs Minisztérium EKÖP-24 kódszámú Egyetemi Kiválósági Ösztöndíj Programjának a Nemzeti Kutatási, Fejlesztési és Innovációs Alapból finanszírozott szakmai támogatásával készült.